
nuggets is a package for R statistical computing
environment providing a framework for systematic exploration of
association rules (Agrawal (1994)),
contrast patterns (Chen (2022)),
emerging patterns (Dong (1999)),
subgroup discovery (Atzmueller (2015)), and
conditional correlations (Hájek (1978)).
User-defined functions may also be supplied to guide custom pattern
searches.
Supports both crisp (Boolean) and fuzzy data. Generates candidate conditions expressed as elementary conjunctions, evaluates them on a dataset, and inspects the induced sub-data for statistical, logical, or structural properties such as associations, correlations, or contrasts. Includes methods for visualization of logical structures and supports interactive exploration through integrated Shiny applications.
Read the full documentation of the nuggets package.
To install the stable version of nuggets from CRAN, type
the following command within the R session:
install.packages("nuggets")You can also install the development version of nuggets
from GitHub with:
install.packages("devtools")
devtools::install_github("beerda/nuggets")To start using the package, load it to the R session with:
library(nuggets)The following example demonstrates how to use nuggets to
find association rules in the built-in mtcars dataset:
# Preprocess: dichotomize and fuzzify numeric variables
cars <- mtcars |>
partition(cyl, vs:gear, .method = "dummy") |>
partition(carb, .method = "crisp", .breaks = c(0, 3, 10)) |>
partition(mpg, disp:qsec, .method = "triangle", .breaks = 3)
# Search for associations among conditions
rules <- dig_associations(cars,
antecedent = everything(),
consequent = everything(),
max_length = 4,
min_support = 0.1)
# Add various interest measures
rules <- add_interest(rules)
# Explore the found rules interactively
explore(rules, cars)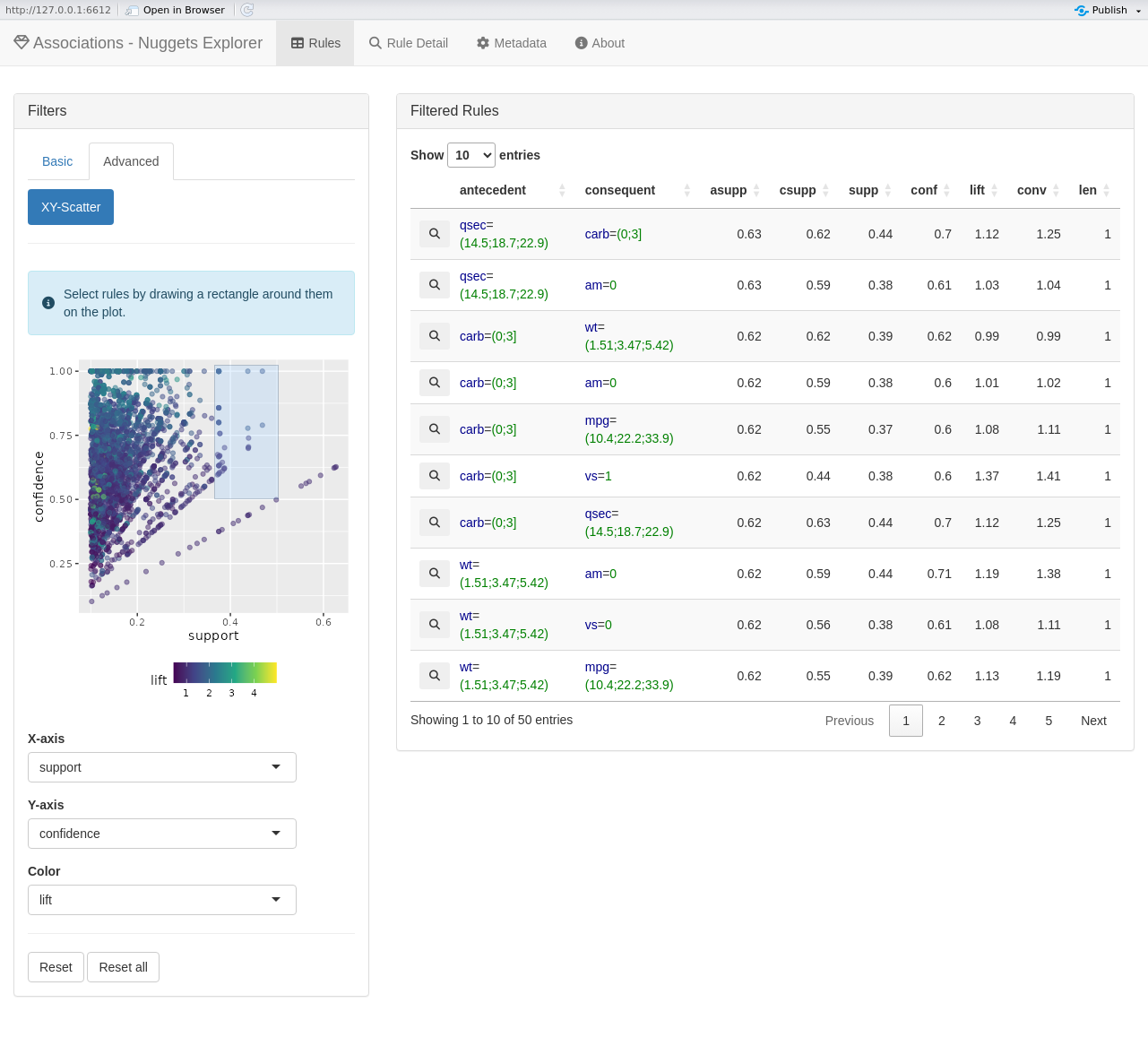
Contributions, suggestions, and bug reports are welcome. Please submit issues on GitHub.
This package is licensed under the GPL-3 license.
It includes third-party code licensed under BSD-2-Clause,
BSD-3-Clause, and GPL-2 or later licenses. See
inst/COPYRIGHTS for details.