The massProps package extends rollupTree
with functions to recursively calculate mass properties (and optionally,
their uncertainties) for arbitrary composition trees. Formulas
implemented are described in a technical paper published by the Society
of Allied Weight Engineers (Zimmerman and Nakai 2005).
install.packages("massProps")You can install the development version of massProps from GitHub with:
# install.packages("pak")
pak::pak("jsjuni/massProps")Suppose we have the following mass properties table:
library(massProps)
test_table
#> id parent mass Cx Cy Cz Ixx Ixy Ixz Iyy Iyz Izz POIconv Ipoint
#> 1 A.1 NA NA NA NA NA NA NA NA NA NA - FALSE
#> 2 A.2 A.1 NA NA NA NA NA NA NA NA NA NA - FALSE
#> 3 A.3 A.1 NA NA NA NA NA NA NA NA NA NA - FALSE
#> 4 C.1 A.1 5 0 0 0 80 -4.0 -24.0 80 -24.0 75 - FALSE
#> 5 P.1 A.2 2 1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 6 P.2 A.2 2 1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 7 P.3 A.2 2 1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 8 P.4 A.2 2 1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 9 P.5 A.3 2 -1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 10 P.6 A.3 2 -1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 11 P.7 A.3 2 -1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 12 P.8 A.3 2 -1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSEPOIconv indicates the products of inertia sign
convention. In the negative convention, for example, \(I_{XY} \equiv -\int{xy \rho \, dV}\). In
the positive convention, \(I_{XY} \equiv
\int{xy \rho \, dV}\).
Ipoint indicates whether this object is to be considered
a point mass. The same algebraic result can be achieved by setting all
moments and products of inertia to zero, but
rollup_mass_props() by default ensures that all leaf items
in the tree have mass properties that correspond to
physically-realizable objects. A zero inertia tensor will fail this
check. Rather than relax the check (which is essential for trustworthy
results), a TRUE value for Ipoint indicates
that the inertia tensor should be excluded from computations.
We construct a graph with edges representing child-parent relations:
library(igraph)
E(test_tree)
#> + 11/11 edges from 7d8200c (vertex names):
#> [1] A.2->A.1 A.3->A.1 C.1->A.1 P.1->A.2 P.2->A.2 P.3->A.2 P.4->A.2 P.5->A.3
#> [9] P.6->A.3 P.7->A.3 P.8->A.3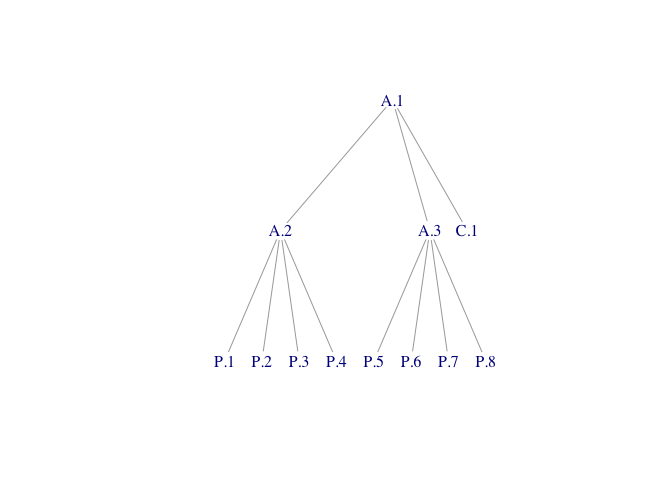
We can roll up mass properties to non-leaf elements as follows:
rollup_mass_props(test_tree, test_table)
#> id parent mass Cx Cy Cz Ixx Ixy Ixz Iyy Iyz Izz POIconv Ipoint
#> 1 A.1 21 0 0 0 144 -4.8 -24.8 144 -23.2 139 - FALSE
#> 2 A.2 A.1 8 1 0 0 32 -0.4 -0.4 24 0.4 24 - FALSE
#> 3 A.3 A.1 8 -1 0 0 32 -0.4 -0.4 24 0.4 24 - FALSE
#> 4 C.1 A.1 5 0 0 0 80 -4.0 -24.0 80 -24.0 75 - FALSE
#> 5 P.1 A.2 2 1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 6 P.2 A.2 2 1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 7 P.3 A.2 2 1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 8 P.4 A.2 2 1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 9 P.5 A.3 2 -1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 10 P.6 A.3 2 -1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 11 P.7 A.3 2 -1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 12 P.8 A.3 2 -1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSENote that, although the table shows the parent of each element for clarity of exposition, the child-parent relations are coneveyed only by the tree passed as the first argument.
The input data may include mass properties uncertainties as well:
test_unc_table
#> id parent mass Cx Cy Cz Ixx Ixy Ixz Iyy Iyz Izz POIconv Ipoint
#> 1 A.1 NA NA NA NA NA NA NA NA NA NA - FALSE
#> 2 A.2 A.1 NA NA NA NA NA NA NA NA NA NA - FALSE
#> 3 A.3 A.1 NA NA NA NA NA NA NA NA NA NA - FALSE
#> 4 C.1 A.1 5 0 0 0 80 -4.0 -24.0 80 -24.0 75 - FALSE
#> 5 P.1 A.2 2 1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 6 P.2 A.2 2 1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 7 P.3 A.2 2 1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 8 P.4 A.2 2 1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 9 P.5 A.3 2 -1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 10 P.6 A.3 2 -1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 11 P.7 A.3 2 -1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 12 P.8 A.3 2 -1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> sigma_mass sigma_Cx sigma_Cy sigma_Cz sigma_Ixx sigma_Iyy sigma_Izz
#> 1 NA NA NA NA NA NA NA
#> 2 NA NA NA NA NA NA NA
#> 3 NA NA NA NA NA NA NA
#> 4 0.5 0.0 0.0 0.0 8.0 8.0 7.5
#> 5 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 6 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 7 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 8 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 9 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 10 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 11 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> 12 0.2 0.1 0.1 0.1 0.4 0.4 0.4
#> sigma_Ixy sigma_Ixz sigma_Iyz
#> 1 NA NA NA
#> 2 NA NA NA
#> 3 NA NA NA
#> 4 0.40 2.40 2.40
#> 5 0.01 0.01 0.01
#> 6 0.01 0.01 0.01
#> 7 0.01 0.01 0.01
#> 8 0.01 0.01 0.01
#> 9 0.01 0.01 0.01
#> 10 0.01 0.01 0.01
#> 11 0.01 0.01 0.01
#> 12 0.01 0.01 0.01Mass properties and their uncertainties can be rolled up as follows:
rollup_mass_props_and_unc(test_tree, test_unc_table)
#> id parent mass Cx Cy Cz Ixx Ixy Ixz Iyy Iyz Izz POIconv Ipoint
#> 1 A.1 21 0 0 0 144 -4.8 -24.8 144 -23.2 139 - FALSE
#> 2 A.2 A.1 8 1 0 0 32 -0.4 -0.4 24 0.4 24 - FALSE
#> 3 A.3 A.1 8 -1 0 0 32 -0.4 -0.4 24 0.4 24 - FALSE
#> 4 C.1 A.1 5 0 0 0 80 -4.0 -24.0 80 -24.0 75 - FALSE
#> 5 P.1 A.2 2 1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 6 P.2 A.2 2 1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 7 P.3 A.2 2 1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 8 P.4 A.2 2 1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 9 P.5 A.3 2 -1 1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 10 P.6 A.3 2 -1 1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 11 P.7 A.3 2 -1 -1 1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> 12 P.8 A.3 2 -1 -1 -1 4 -0.1 -0.1 4 0.1 4 - FALSE
#> sigma_mass sigma_Cx sigma_Cy sigma_Cz sigma_Ixx sigma_Iyy sigma_Izz
#> 1 0.7549834 0.03809524 0.03809524 0.03809524 8.313844 8.275264 7.792946
#> 2 0.4000000 0.05000000 0.07071068 0.07071068 1.600000 1.200000 1.200000
#> 3 0.4000000 0.05000000 0.07071068 0.07071068 1.600000 1.200000 1.200000
#> 4 0.5000000 0.00000000 0.00000000 0.00000000 8.000000 8.000000 7.500000
#> 5 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 6 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 7 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 8 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 9 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 10 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 11 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> 12 0.2000000 0.10000000 0.10000000 0.10000000 0.400000 0.400000 0.400000
#> sigma_Ixy sigma_Ixz sigma_Iyz
#> 1 1.0586784 2.5924506 2.5924506
#> 2 0.4004997 0.4004997 0.6931089
#> 3 0.4004997 0.4004997 0.6931089
#> 4 0.4000000 2.4000000 2.4000000
#> 5 0.0100000 0.0100000 0.0100000
#> 6 0.0100000 0.0100000 0.0100000
#> 7 0.0100000 0.0100000 0.0100000
#> 8 0.0100000 0.0100000 0.0100000
#> 9 0.0100000 0.0100000 0.0100000
#> 10 0.0100000 0.0100000 0.0100000
#> 11 0.0100000 0.0100000 0.0100000
#> 12 0.0100000 0.0100000 0.0100000