

Title: Higher-Level Interface of ‘torch’ Package to Auto-Train Neural Networks
Whether you’re generating neural network architectures expressions or
fitting/training actual models, {kindling} minimizes
boilerplate code while preserving {torch}. Since this
package uses {torch} as its backend, GPU/TPU devices also
supported.
{kindling} also bridges the gap between
{torch} and {tidymodels}. It works seamlessly
with {parsnip}, {recipes}, and
{workflows} to bring deep learning into your existing
{tidymodels} modeling pipeline. This enables a streamlined
interface for building, training, and tuning deep learning models within
the familiar {tidymodels} ecosystem.
{torch} expression{tidymodels}, {mlr3} for later) workflows and
pipelines{torch} tensors
You can install {kindling} on CRAN:
install.packages('kindling')Or install the development version from GitHub:
# install.packages("pak")
pak::pak("joshuamarie/kindling")
## devtools::install_github("joshuamarie/kindling") {kindling} is powered by R’s metaprogramming
capabilities through code generation. Generated
torch::nn_module() expressions power the training
functions, which in turn serve as engines for {tidymodels}
integration. This architecture gives you flexibility to work at whatever
abstraction level suits your task.
library(kindling)
#>
#> Attaching package: 'kindling'
#> The following object is masked from 'package:base':
#>
#> argsBefore starting, you need to install LibTorch, the backend of PyTorch
which also the backend of {torch} R package:
torch::install_torch()torch::nn_moduleAt the lowest level, you can generate raw
torch::nn_module code for maximum customization. Functions
ending with _generator return unevaluated expressions you
can inspect, modify, or execute.
Here’s how to generate a feedforward network specification:
ffnn_generator(
nn_name = "MyFFNN",
hd_neurons = c(64, 32, 16),
no_x = 10,
no_y = 1,
activations = 'relu'
)
#> torch::nn_module("MyFFNN", initialize = function ()
#> {
#> self$fc1 = torch::nn_linear(10, 64, bias = TRUE)
#> self$fc2 = torch::nn_linear(64, 32, bias = TRUE)
#> self$fc3 = torch::nn_linear(32, 16, bias = TRUE)
#> self$out = torch::nn_linear(16, 1, bias = TRUE)
#> }, forward = function (x)
#> {
#> x = self$fc1(x)
#> x = torch::nnf_relu(x)
#> x = self$fc2(x)
#> x = torch::nnf_relu(x)
#> x = self$fc3(x)
#> x = torch::nnf_relu(x)
#> x = self$out(x)
#> x
#> })This creates a three-hidden-layer network (64 - 32 - 16 neurons) that takes 10 inputs and produces 1 output. Each hidden layer uses ReLU activation, while the output layer remains “untransformed”.
Skip the code generation and train models directly with your data.
This approach handles all the {torch} boilerplate when
training the models internally.
Let’s classify iris species:
model = ffnn(
Species ~ .,
data = iris,
hidden_neurons = c(10, 15, 7),
activations = act_funs(relu, softshrink = args(lambd = 0.5), elu),
loss = "cross_entropy",
epochs = 100
)
model======================= Feedforward Neural Networks (MLP) ======================
-- FFNN Model Summary ----------------------------------------------------------
-----------------------------------------------------------------------
NN Model Type : FFNN n_predictors : 4
Number of Epochs : 100 n_response : 3
Hidden Layer Units : 10, 15, 7 reg. : None
Number of Hidden Layers : 3 Device : cpu
Pred. Type : classification :
-----------------------------------------------------------------------
-- Activation function ---------------------------------------------------------
-------------------------------------------------
1st Layer {10} : relu
2nd Layer {15} : softshrink(lambd = 0.5)
3rd Layer {7} : elu
Output Activation : No act function applied
-------------------------------------------------Evaluate the prediction through predict(). The
predict() method is extended for fitted models through its
newdata argument.
Two kinds of predict() usage:
Without newdata predictions is the
default to the parent data frame.
predict(model) |>
(\(x) table(actual = iris$Species, predicted = x))()
#> predicted
#> actual setosa versicolor virginica
#> setosa 50 0 0
#> versicolor 0 46 4
#> virginica 0 2 48With newdata simply pass the new
data frame as the new reference.
sample_iris = dplyr::slice_sample(iris, n = 10, by = Species)
predict(model, newdata = sample_iris) |>
(\(x) table(actual = sample_iris$Species, predicted = x))()
#> predicted
#> actual setosa versicolor virginica
#> setosa 10 0 0
#> versicolor 0 10 0
#> virginica 0 1 9Work with neural networks just like any other {parsnip}
model. This unlocks the entire {tidymodels} toolkit for
preprocessing, cross-validation, and model evaluation.
# library(kindling)
# library(parsnip)
# library(yardstick)
box::use(
kindling[mlp_kindling, rnn_kindling, act_funs, args],
parsnip[fit, augment],
yardstick[metrics],
mlbench[Ionosphere] # data(Ionosphere, package = "mlbench")
)
ionosphere_data = Ionosphere[, -2]
# Train a feedforward network with parsnip
mlp_kindling(
mode = "classification",
hidden_neurons = c(128, 64),
activations = act_funs(relu, softshrink = args(lambd = 0.5)),
epochs = 100
) |>
fit(Class ~ ., data = ionosphere_data) |>
augment(new_data = ionosphere_data) |>
metrics(truth = Class, estimate = .pred_class)
#> # A tibble: 2 × 3
#> .metric .estimator .estimate
#> <chr> <chr> <dbl>
#> 1 accuracy binary 0.989
#> 2 kap binary 0.975
# Or try a recurrent architecture (demonstrative example with tabular data)
rnn_kindling(
mode = "classification",
hidden_neurons = c(128, 64),
activations = act_funs(relu, elu),
epochs = 100,
rnn_type = "gru"
) |>
fit(Class ~ ., data = ionosphere_data) |>
augment(new_data = ionosphere_data) |>
metrics(truth = Class, estimate = .pred_class)
#> # A tibble: 2 × 3
#> .metric .estimator .estimate
#> <chr> <chr> <dbl>
#> 1 accuracy binary 0.641
#> 2 kap binary 0The package has integration with {tidymodels}, so it
supports hyperparameter tuning via {tune} with searchable
parameters.
The current searchable parameters under {kindling}:
The searchable parameters outside from {kindling},
i.e. under {dials} package such as
learn_rate() also supported.
Here’s an example:
# library(tidymodels)
box::use(
kindling[
mlp_kindling, hidden_neurons, activations, output_activation, grid_depth
],
parsnip[fit, augment],
recipes[recipe],
workflows[workflow, add_recipe, add_model],
rsample[vfold_cv],
tune[tune_grid, tune, select_best, finalize_workflow],
dials[grid_random],
yardstick[accuracy, roc_auc, metric_set, metrics]
)
mlp_tune_spec = mlp_kindling(
mode = "classification",
hidden_neurons = tune(),
activations = tune(),
output_activation = tune()
)
iris_folds = vfold_cv(iris, v = 3)
nn_wf = workflow() |>
add_recipe(recipe(Species ~ ., data = iris)) |>
add_model(mlp_tune_spec)
nn_grid_depth = grid_depth(
hidden_neurons(c(32L, 128L)),
activations(c("relu", "elu")),
output_activation(c("sigmoid", "linear")),
n_hlayer = 2,
size = 10,
type = "latin_hypercube"
)
# This is supported but limited to 1 hidden layer only
## nn_grid = grid_random(
## hidden_neurons(c(32L, 128L)),
## activations(c("relu", "elu")),
## output_activation(c("sigmoid", "linear")),
## size = 10
## )
nn_tunes = tune::tune_grid(
nn_wf,
iris_folds,
grid = nn_grid_depth
# metrics = metric_set(accuracy, roc_auc)
)
best_nn = select_best(nn_tunes)
final_nn = finalize_workflow(nn_wf, best_nn)
# Last run: 4 - 91 (relu) - 3 (sigmoid) units
final_nn_model = fit(final_nn, data = iris)
final_nn_model |>
augment(new_data = iris) |>
metrics(truth = Species, estimate = .pred_class)
#> # A tibble: 2 × 3
#> .metric .estimator .estimate
#> <chr> <chr> <dbl>
#> 1 accuracy multiclass 0.667
#> 2 kap multiclass 0.5Resampling strategies from {rsample} will enable robust
cross-validation workflows, orchestrated through the {tune}
and {dials} APIs.
{kindling} integrates with established variable
importance methods from {NeuralNetTools} and
{vip} to interpret trained neural networks. Two primary
algorithms are available:
Garson’s Algorithm
garson(model, bar_plot = FALSE)
#> x_names y_names rel_imp
#> 1 Sepal.Width y 29.04598
#> 2 Petal.Width y 27.50590
#> 3 Sepal.Length y 24.20982
#> 4 Petal.Length y 19.23830Olden’s Algorithm
olden(model, bar_plot = FALSE)
#> x_names y_names rel_imp
#> 1 Sepal.Width y 0.56231712
#> 2 Petal.Width y -0.51113650
#> 3 Petal.Length y -0.29761552
#> 4 Sepal.Length y -0.06857191For users working within the {tidymodels} ecosystem,
{kindling} models work seamlessly with the
{vip} package:
box::use(
vip[vi, vip]
)
vi(model) |>
vip()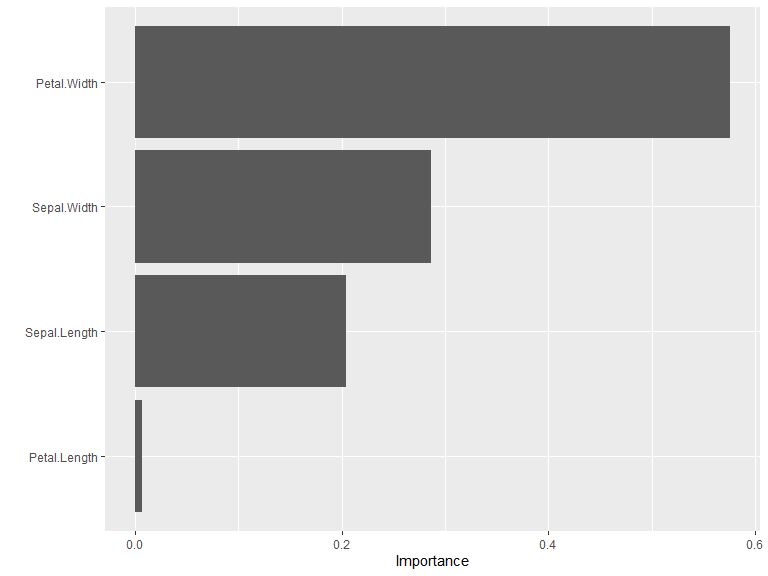
Note: Weight caching increases memory usage proportional to network size. Only enable it when you plan to compute variable importance multiple times on the same model.
Falbel D, Luraschi J (2023). torch: Tensors and Neural Networks with ‘GPU’ Acceleration. R package version 0.13.0, https://torch.mlverse.org, https://github.com/mlverse/torch.
Wickham H (2019). Advanced R, 2nd edition. Chapman and Hall/CRC. ISBN 978-0815384571, https://adv-r.hadley.nz/.
Goodfellow I, Bengio Y, Courville A (2016). Deep Learning. MIT Press. https://www.deeplearningbook.org/.
MIT + file LICENSE
Please note that the kindling project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.