The library Rnest offers the Next Eigenvalue Sufficiency
Tests (NEST; Achim, 2017; 2020) to determine the number of dimensions in
exploratory factor analysis. It provides a main function
nest() to carry the analysis, a plot()
function a many utilit. It has been showed to amongst the best stopping
rule to determine the nuber of factor in factor analysis (Achim, 2021;
Brandenburg & Papenberg, 2024; Caron, 2025).
There is many examples of correlation matrices available with the
packages and other stopping rules as well, such as PA() for
parallel analysis or MAP() for minimum average partial
correlation.
As of version 1.0, Rnest is compatible with
the tidyverse and the %>%.
The development version can be accessed through GitHub:
remotes::install_github(repo = "quantmeth/Rnest")
library(Rnest)The CRAN package is also available.
installed.packages("Rnest")
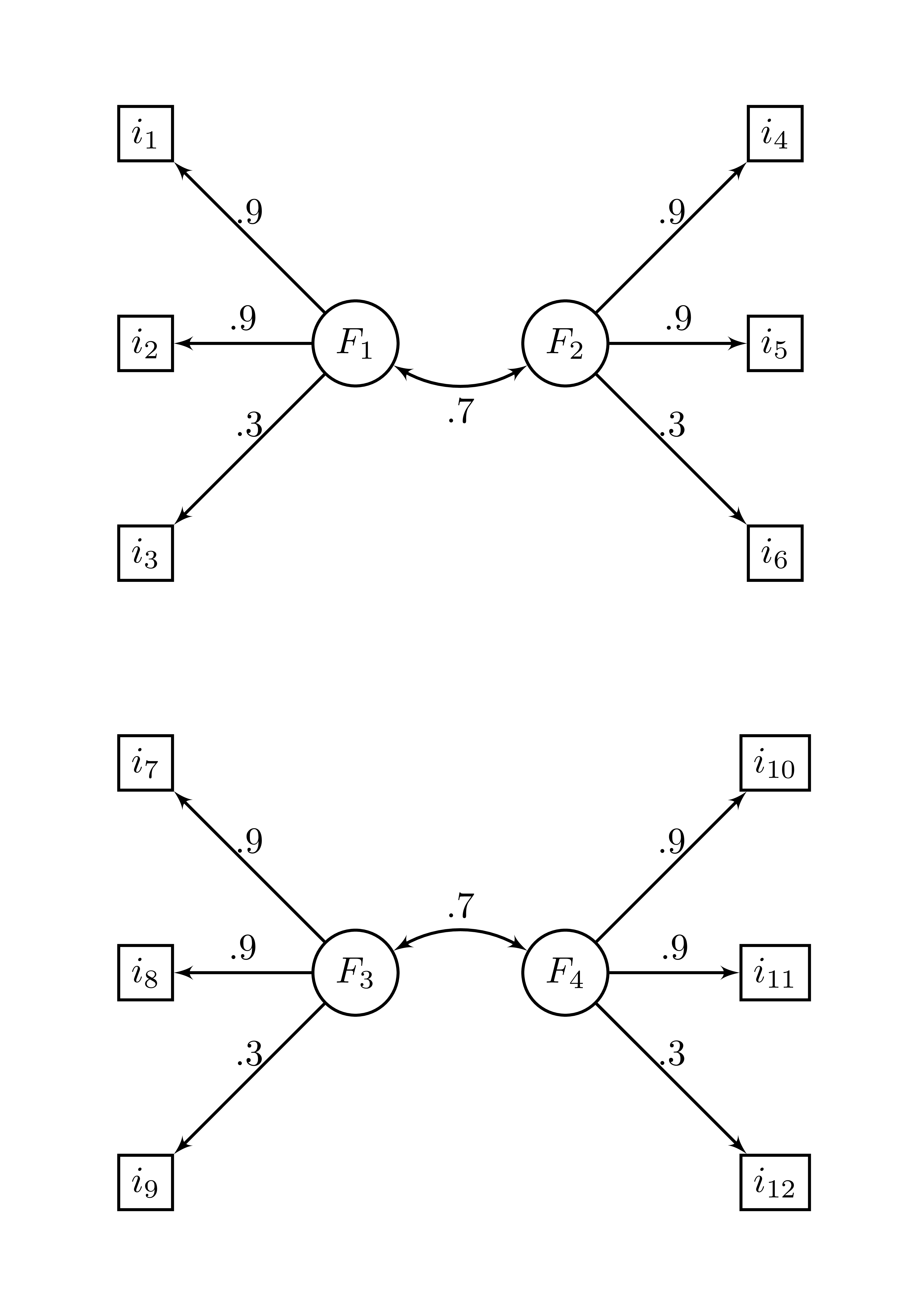
library(Rnest)Here is an example using the ex_4factors_corr
correlation matrix from the Rnest library. The factor
structure is

and the correlation matrix is
\[\begin{bmatrix} 1&.810&.270&.567&.567&.189&&&&&& \\ .810&1&.270&.567&.567&.189&&&&&& \\ .270&.270&1&.189&.189&.063&&&&&& \\ .567&.567&.189&1&.810&.270&&&&&& \\ .567&.567&.189&.810&1&.270&&&&&& \\ .189&.189&.063&.270&.270&1&&&&&& \\ &&&&&&1&.810&.270&.567&.567&.189 \\ &&&&&&.810&1&.270&.567&.567&.189 \\ &&&&&&.270&.270&1&.189&.189&.063 \\ &&&&&&.567&.567&.189&1&.810&.270 \\ &&&&&&.567&.567&.189&.810&1&.270 \\ &&&&&&.189&.189&.063&.270&.270&1 \\ \end{bmatrix}\]
From ex_4factors_corr, we can easily generate random
data using the MASS packages (Venables & Ripley,
2002).
set.seed(1)
mydata <- MASS::mvrnorm(n = 2500,
mu = rep(0, ncol(ex_4factors_corr)),
Sigma = ex_4factors_corr)We can then carry NEST.
res <- nest(mydata)
res## Next Eigenvalue Sufficiency Test (NEST) suggests 4 factors.The first output tells hom many factors NEST suggests. We can also consult the summary with
summary(res)##
## nest 1.1 ended normally
##
## Estimator ML
## Missing data treatment FIML
## Number of model parameters 66
## Resampling 1000
## Sample size 2500
## Stopped at 5
##
##
## Test that k factors are sufficient
##
## k factor NextEig CritEig Prob
## k = 0 3.228 1.155 < .001
## k = 1 3.167 1.113 < .001
## k = 2 1.007 0.993 .010
## k = 3 0.972 0.958 .009
## k = 4 0.860 0.903 .727
##
##
## Next Eigenvalue Sufficiency Test (NEST) suggests 4 factors.
##
## Try plot(nest()) to see a graphical representation of the results.
## We can visualize the results using the generic function
plot() using the nest() output.
plot(res)
Scree plot of NEST
The above figure shows the empirical eigenvalues in blue and the 95th percentile of the sampled eigenvalues.
It is also possible to use a correlation matrix directly. A sample
size, n must be supplied.
nest(ex_4factors_corr, n = 240)## Next Eigenvalue Sufficiency Test (NEST) suggests 2 factors.The nest() function can use with many \(\alpha\) values and presents parallel
analysis results if desired.
res <- nest(ex_4factors_corr, n = 120, alpha = c(.01,.025,.05))
plot(res, pa = TRUE)
Scree plot of NEST with many \(\alpha\)
Recommended usage : fiml estimation for correlation matrix and removing unique variables.
library(dplyr)
ex_3factors_doub_unique %>%
genr8(n = 200) %>% # to generate simulated data for the example
cor_nest() %>%
remove_unique() %>%
nest() %>%
plot(pa = TRUE)
Caron, P.-O. (2025). Rnest: An R package for the Next Eigenvalue Sufficiency Test. https://github.com/quantmeth/Rnest